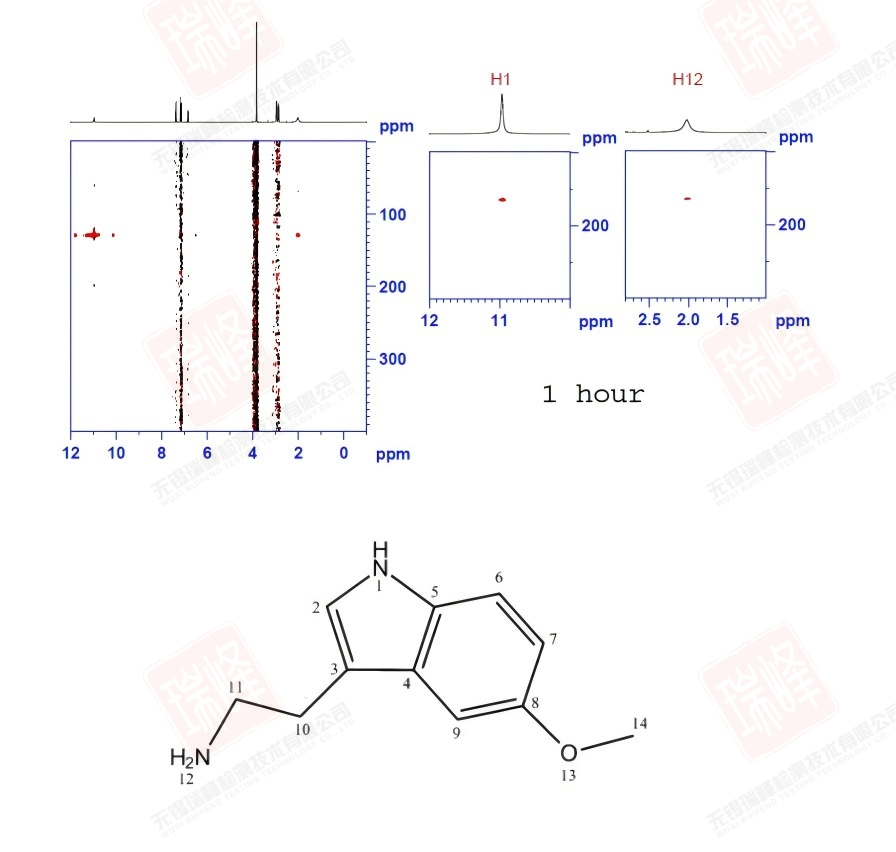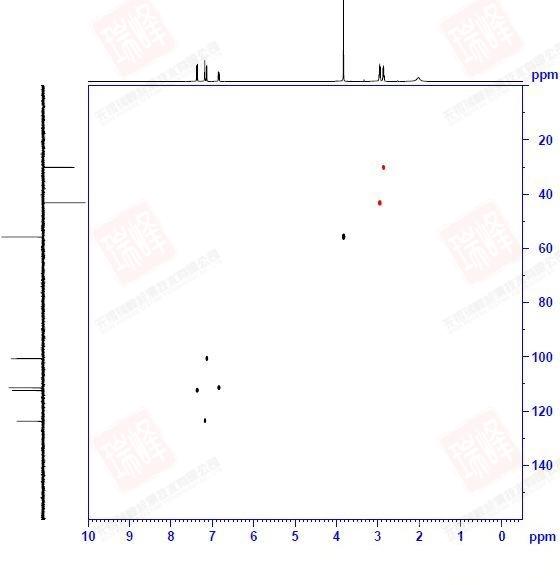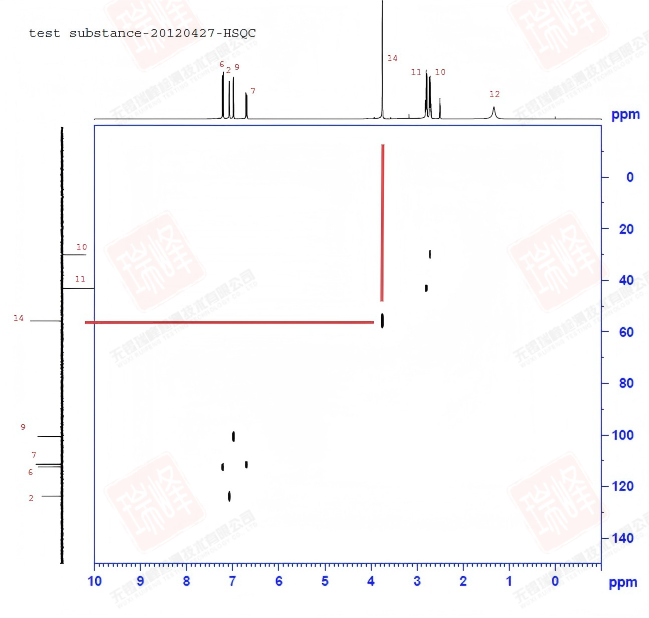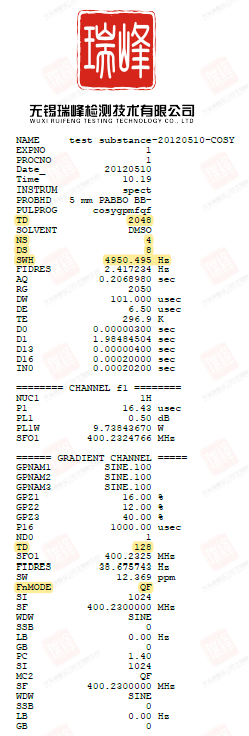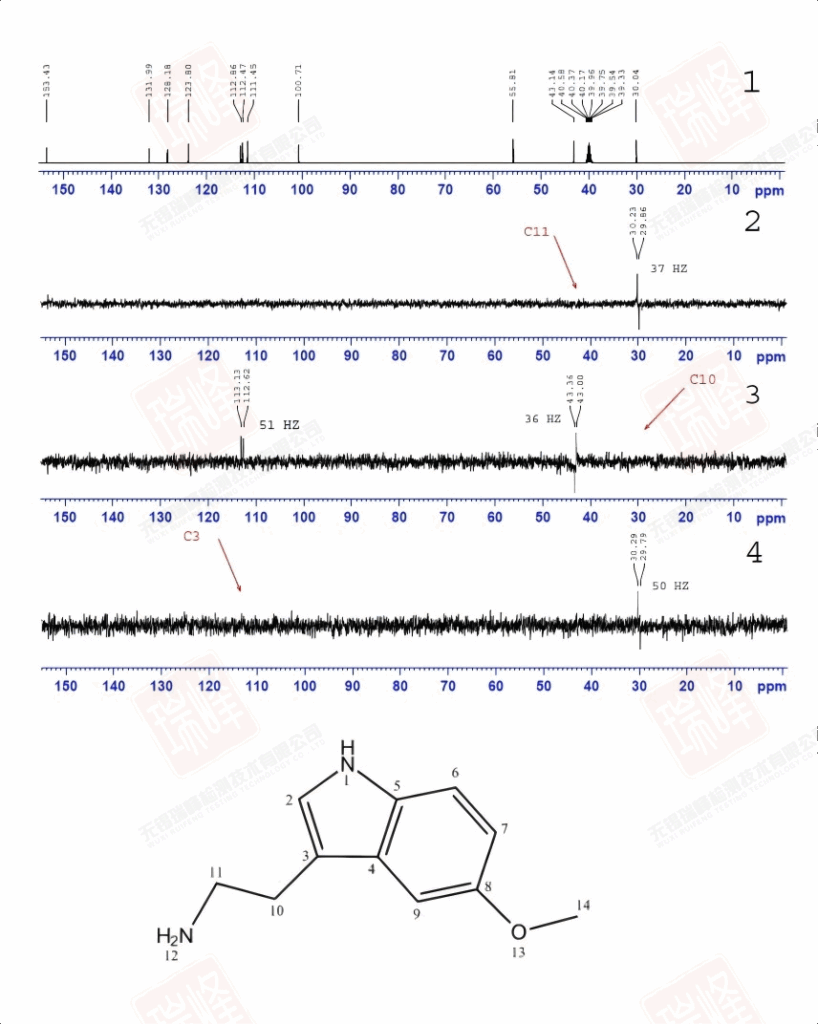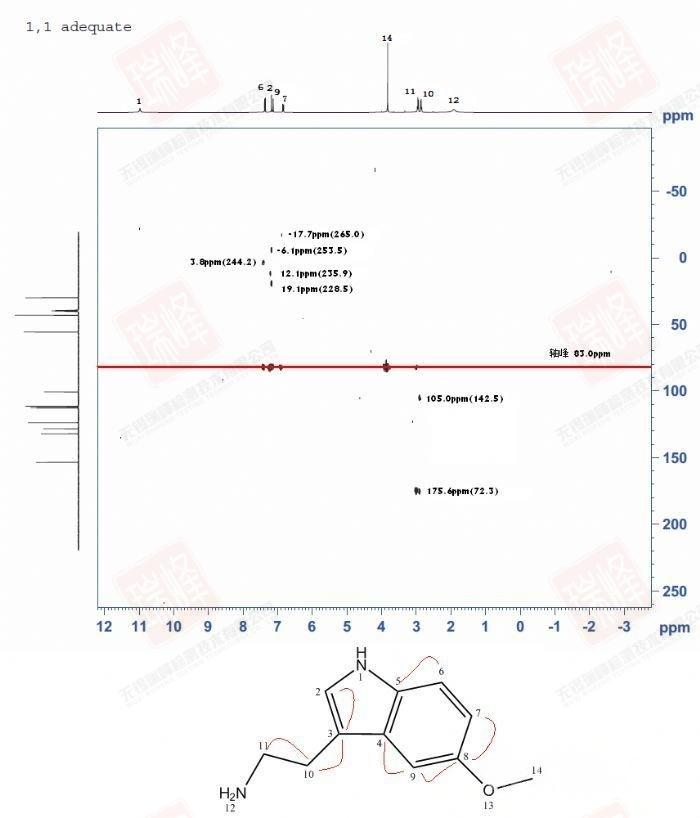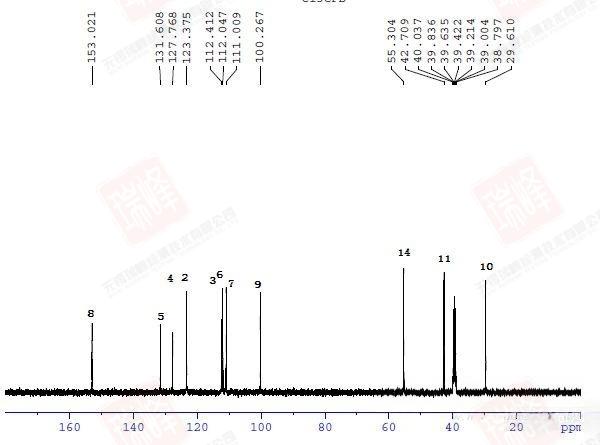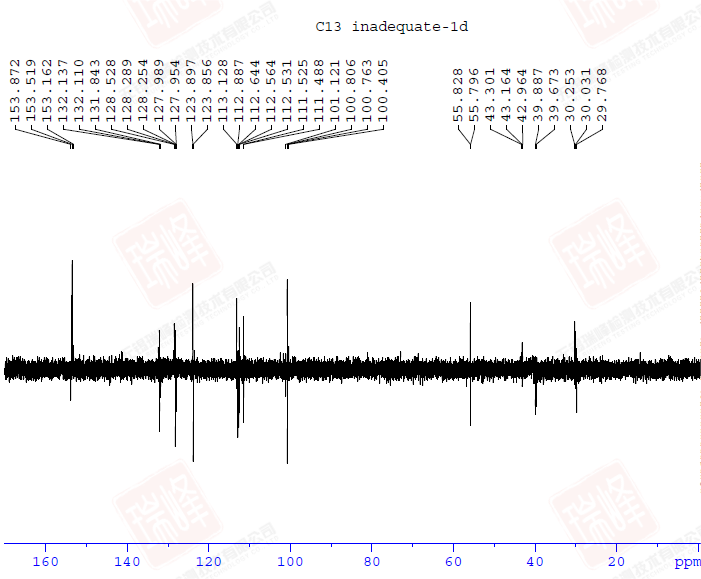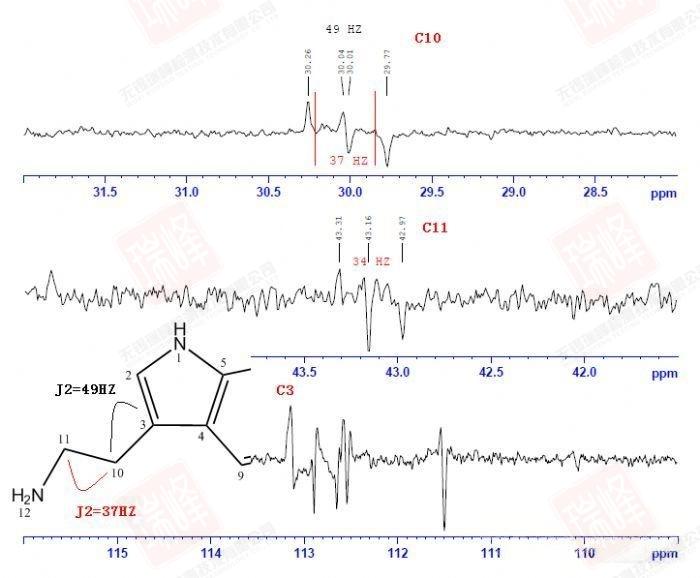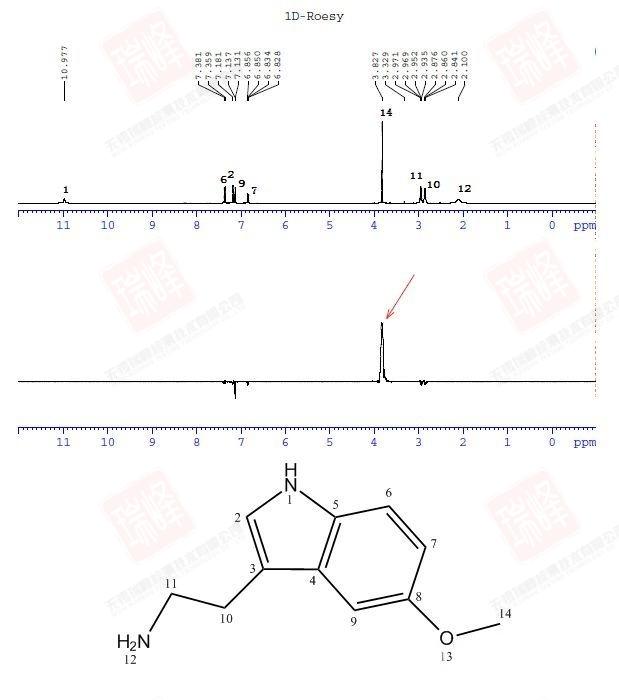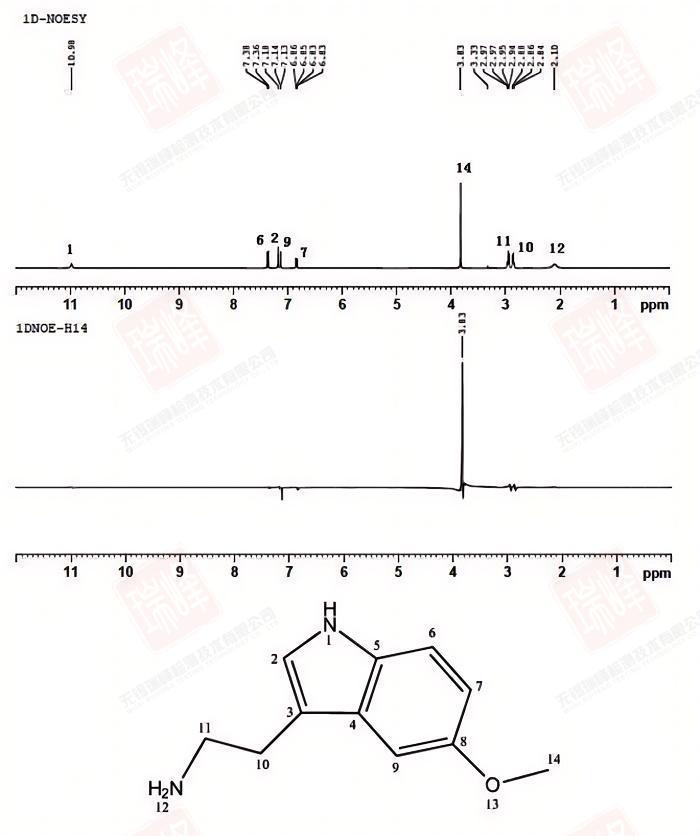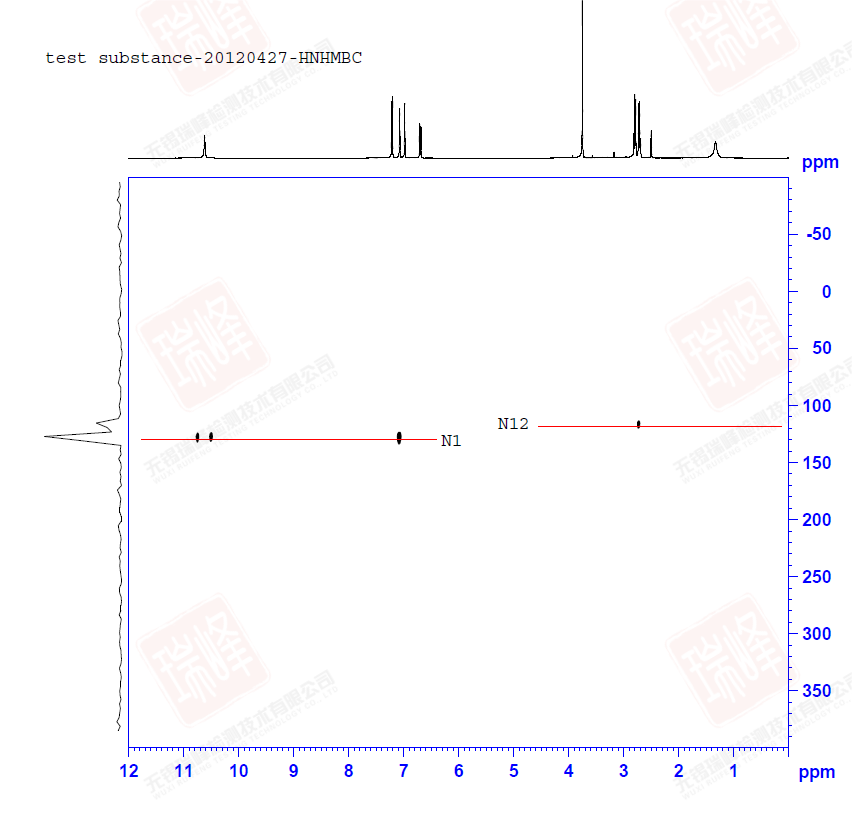
同大家所熟知的H-C HMBC一样，H-N HMBC给出的是H-N远程耦合的信息。为了便于分析，我将谱图的信号部分单独放大。

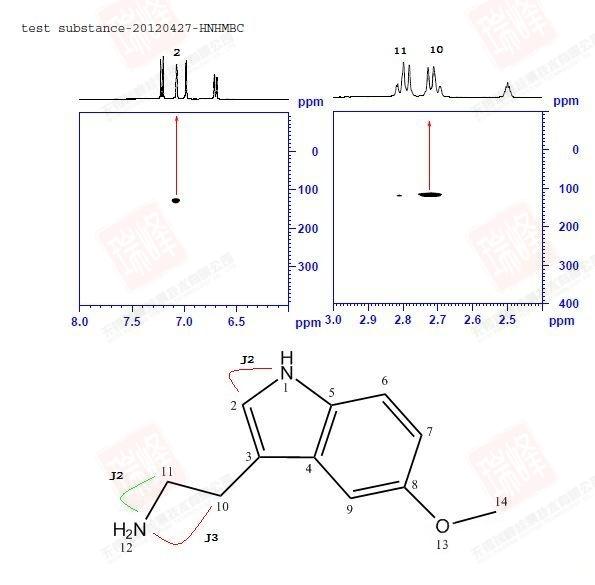
同HSQC相同之处在于H-N HMBC给出的同样是¹⁵N和¹H之间的相关信息，谱图中每一个点所对应的F2维H及F1维N在结构上有相关性；但同HSQC的不同之处在于，HMBC给出的是H-N远程耦合的信息，H-N一键相关的信号在谱图上常以耦合形式出现（如图中N₁所对应的在10-11 ppm围绕H₁对称出现的点）或干脆消失（如结构中端位的NH₂）。但这里要消除的一个关于HMBC的误区是，很多人都认为信号的强度与耦合经历的键数成反比：J2耦合信号强于J3，而J3强于J4，以此类推……然而事实是，C/N-H的耦合常数并不完全取决于传递键的个数(通常而言，J2耦合X-Y-X角大，耦合值大，J3耦合值受所成二面角的影响，而J4，J5耦合值常常相等)；而不同耦合值在HMBC中信号的强弱还受到脉冲序列中一个设定参数(CNST13)的影响。总体而言，J3耦合较J2耦合在HMBC中的信号有时会更强一些，而J2有时并不出现，J4，J5无法区分。

本实验中的N₁与H₂的J2信号在谱图中很明显，而N₁₂与H₁₀的J3耦合信号要远强于其与H₁₁的J2耦合，这导致我一度在信号归属中将H₁₀与H₁₁的归属标反（结合前面H谱分析中关于¹⁴N核四极矩引起谱线增宽的判断，这一决定让我着实犹豫了很久），但最终在之后明确的证据下我还是选择了目前的标法，这一点我之后会细谈。

H-N HSQC给出的是H与N一键相关的信息。解谱方式参照H-C HSQC。

这一实验的魅力在于，利用反向检测技术，将不灵敏核¹⁵N的信息转移到灵敏核¹H，极大地缩短了¹⁵N信号出峰的时间：通常而言¹⁵N谱所需要的样品浓度非常之高，而普通样品的¹⁵N谱花费数天甚至数星期都是很有可能的，但本实验只用了不到1h就得到了较为满意的结果 。由于N元素在有机物尤其是生物大分子中大量出现，这一实验在结构指认方面的重要性不言而喻。

这里插一句，也许大家会想到既然¹⁵N在自然界的丰度如此之低(0.366%)，为何不直接采集¹⁴N(99.634%)的核磁信号呢？事实上这是核磁科学家的无奈之举。我们知道，自旋数不为0的核能够被核磁检测出来，然而只有自旋数为1/2的核才能被当做点电荷处理，而其他非0自旋核在磁场中都不得不考虑一种称为核四极矩的电场不均匀效应。幸运的是，对于有些核而言，核四极矩并不会对信号由太大干扰（如我之后将介绍的氘谱），但对于绝大多数核，核四极矩将严重影响谱线的线型，而¹⁴N正是这些核的典型：大部分情况下，¹⁴N的核磁信号将会展宽到无法被观察到。因此，科学家不得不转向丰度低的多的¹⁵N来寻求N元素的信息。

这一HSQC与前面所介绍的相比，能够给出更多的信息：CH及CH₃类型的碳氢一键相关，图中出现的点为“正”；CH₂类型的相关，则给出“负”的相关信号，正负信号由两种不同的颜色在谱图上区分（如上图中的黑色和红色）。这一规律同DEPT135相当类似，但也有同样的问题——相位是可以校正的，所以如果发现颜色与预期相反，要求操作人员把峰矫正回来就是了。

事实上，这一谱图可以取代传统的H-C HSQC，甚至可以部分取代DEPT135的作用。如果在做完氢谱之后再给我5分钟的话，我会顺手做个edit的HSQC。

在得到了氢谱和碳谱信息之后，如何将他们关联起来成了一个主要的问题：较碳谱而言，氢谱能给出相邻核之间的耦合值，因此在归属上能够给出更明确的信息；而与氢谱比较，碳谱因为谱宽分布大的多，因此当氢谱中由于化学位移相近而严重重叠时，往往能够在碳谱一维得到很好的区分。而有一种实验能够将两者完美的关联在一起，令人兴奋的是，这一实验是成功率最高的二维实验之一，同时他所需要的时间极短，往往在5-10分钟内就能得到很好的结果。如此实用的一个实验，没有理由不记住它的名字：HSQC。

上图即是这一化合物的HSQC谱图。作为本帖出现的第一个二维谱图，HSQC开了个好头：如图所示，它的结果是明确和令人愉悦的。横的一维称作F2维又叫直接维，从下面的坐标范围可以清楚的看到，它描述的是氢维度的信息，顶部的氢谱明确了H各个峰的位置（顶部谱图是单独做了氢谱后载入的，单纯的HSQC实验给出的投影往往没有这么好）；而纵向的维度称为F1维又叫间接维，它描述的是碳谱的信息。由于这一维度并不是由采样直接获得，因此分辨率一般较差（与提高F2维分辨率相比，间接维的分辨率提升需要付出更多的实验时间）。好在碳谱不差分辨率。正如图中所看到的那样，图中的信号往横和纵两个方向可以分别在氢谱和碳谱上找到对应的峰，而碳和与之直接相连的氢也就因此关联了起来。正如红色线段所标示的那样，H₁₄和C₁₄的关系出现在了它最应该出现的位置。而再花上不到1分钟的时间，我们就可以将所有H和C“绑定”在了一起。

这里我想插一句的是，在很多教材上，有一个与之相类似的实验HMQC。某种程度上，可以认为HSQC是HMQC的某种进化，两者在解谱上面没有任何区别。一般而言，当你的仪器性能比较正常的时候，HSQC比HMQC的分辨率要好一些。但HMQC的优势在于它的脉冲序列更为简单：因此如果核磁谱仪非常老，或者脉冲角度不太准的时候，HMQC的图也许好一些；但大部分情况下，如果你看文献上面是HMQC实验而核磁操作人员给你出的是HSQC的谱图，并没有什么问题。

讲到这里，大家也许会奇怪。既然HSQC能够同时给出H谱和C谱的信息，那理论上它的实验时间至少应该和C谱相当，为什么它所花费的采样时间却远低于碳谱呢？其实，这才是HSQC的魅力所在！已知H的旋磁比是C₁₃的4倍，由于核磁信噪比正比于旋磁比的5/2次方，而这一实验从激发到采样都只和H有关，那么从理论上这一增强即是32倍——这还是相当可观的。这一技术被称作反向检测，被广泛应用在许多二维实验中，今后会大量遇到，尤其是在一些比C丰度更小，旋磁比更低的核（如N₁₅）上，HSQC实验能使在短时间内对N核的检测从不可能变为可能。这一部分我将在之后细说。

再讲两个HSQC的实用应用。

由于HSQC采用的反向检测技术使碳维信息的给出时间大为缩短，因此当想在短时间初略观察碳（非季碳）时，HSQC是一个很好的选择。我曾经尝试过利用软件将HSQC在F1维的投影单独抽取出来以碳谱形式呈现，效果也是不错的！

另外，关于活泼氢的判断，教科书往往把重水交换作为一个主要内容。其实，相对于重水交换取出样品加入重水再充分交换匀场做样而言，我更习惯直接在氢谱后排个HSQC了事，而很多时候这样没准更快。因为HSQC给出的是HC直接相关的信息，当有一个H信号没有与之相关的C相连时，结合它的峰型和出峰位置，基本可以做出是活泼氢的判断。

以COSY为例简单讲一下解谱人员感兴趣的二维实验参数设置部分。

TD2：即图中上数第一个TD是F2维采样维度的采样点数，取值大，F2维fid分辨率就越大。二维实验中这一值的变化对实验时间影响不大，但通常而言没有必要取太大值。

NS：累加次数。这一值仅作用于采样维——值越大，信号信噪比越大，对于NOESY,HMBC这类信噪比比较低的实验可以通过增加NS值使原先不出的信号出现。但NS的大小直接关系到实验时间(NS加倍，实验总时间加倍)。

DS：空扫次数。普通一维实验中同样有空扫次数的设定，但是在二维实验中往往更为重要。适当的空扫能使系统在正式采样前进入相对平衡的状态。

SWH：谱宽。F2维和F1维有各自的谱宽，其取值将直接决定实验观测的谱图范围。

TD1：图中第二个TD是F1维间接维的采样点数。这是二维实验所特有的参数，其取值直接影响F1维的分辨率。由于TD1和NS一样直接影响到实验时间，因此通常限于时间并不能取太大数值。但有些时候，当F1维峰之间化学位移相近时，为了做出正确判断，增加TD1是必须的。

FnMODE：这是间接维的采样模式。常见的QF采样使得二维谱的峰相位不可调。

总体而言，在直接采样维度(F2维)二维谱的TD,NS,DS,SWH等参数与一维谱意义相同，但间接维的一些参数有其特有的意义。