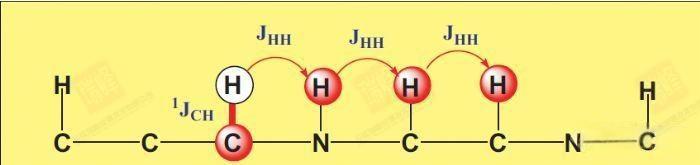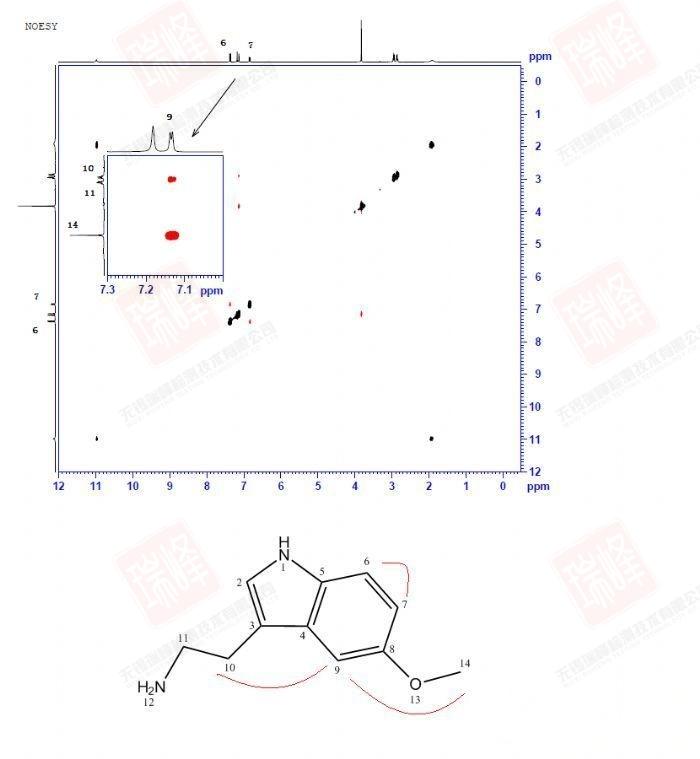
NOESY上相关信号描述的是化合物H之间空间距离的远近关系，与COSY,TOCSY等依赖化学键传递不同，不同H之间即使相隔多键，只要他们空间上相互接近(如下图)，就可以在NOESY谱图上找到相关点。

图中的NOE是Nuclear Overhauser Effect的缩写，之前在讨论C13CPD中曾经出现过，是指当照射H核时邻近C核的谱峰也相应增强，而在同核中这一效应同样存在：当照射H核时，与其空间上小于4A(埃)的H信号会获得轻微的增强(不超过20%)并被检测到，该效应强烈依赖空间距离(与距离的6次方成反比)。凭借这一特殊性质，NOESY实验成为了化学家，生物学家们研究分子空间结构以及生物大分子结构与功能关系的强大工具。

但NOESY要做成功并不容易。NOE效应与分子本身有关，一般在NOESY谱图中将对角峰调为正吸收，此时NOE信号在谱图上的正负取决于一个与分子运动状况相关的参数(慢运动条件下为正峰，快运动条件下为负峰)，但尴尬的是当这一运动正好处在一个不快不慢的状态时，即使相隔很近的H之间也无法观察到NOE效应。由于分子运动状况常和分子大小相关，因此NOESY更适合于大分子和小分子，而我们最常遇到的中等分子信号增强往往很弱。不过，之后提到的ROESY实验可以克服这方面的问题。

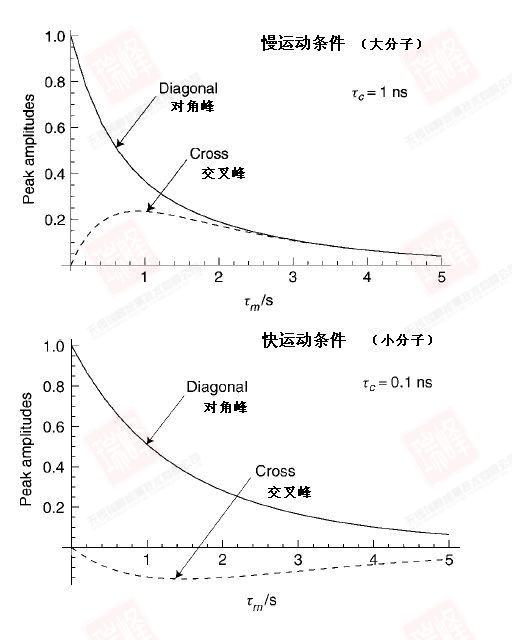
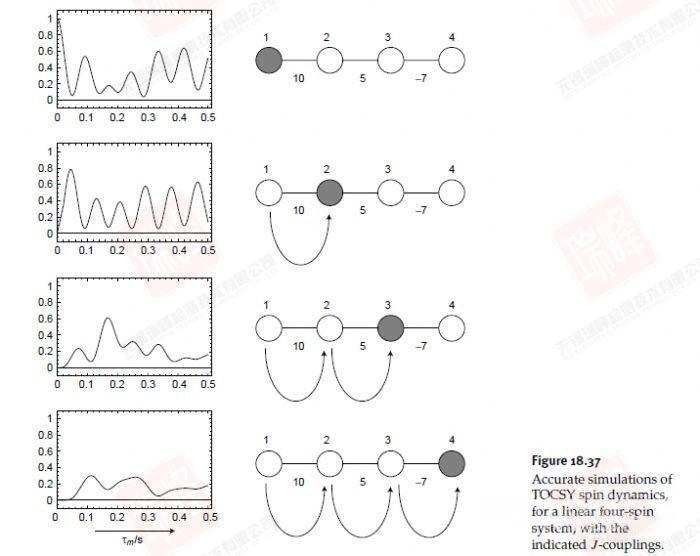
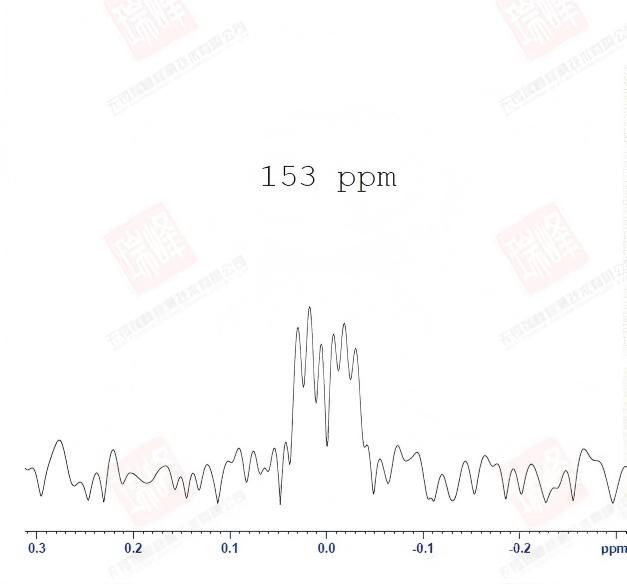
在日常应用中，NOESY的实验参数优化就是混合时间的优化。上图中横坐标为混合时间，虚线为不同混合时间对应下交叉峰的强弱，可以看到对于不同大小的分子，存在一个最优的混合时间使交叉峰最强(一般分子量大的最优混合时间短)。通常，这个时间接近于分子各峰平均的纵向弛豫时间T1，针对我们的化合物，我通过零点法优化混合时间如下

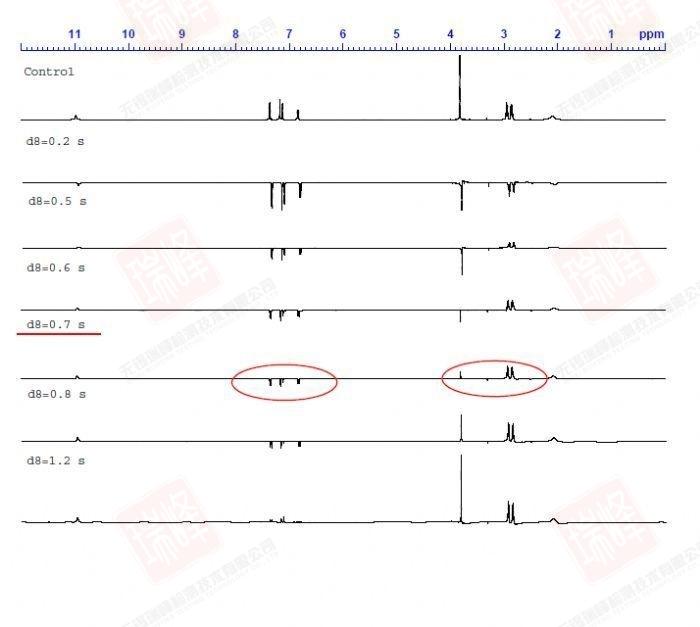
d8是反转恢复后的等待时间。比较而言，在0.7秒时大部分峰接近于零点，零点法公式可以估算出1.0秒为系统的平均T1，这也是我优化后的混合时间。

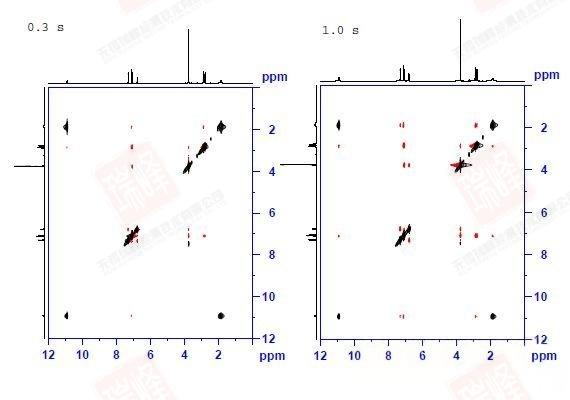
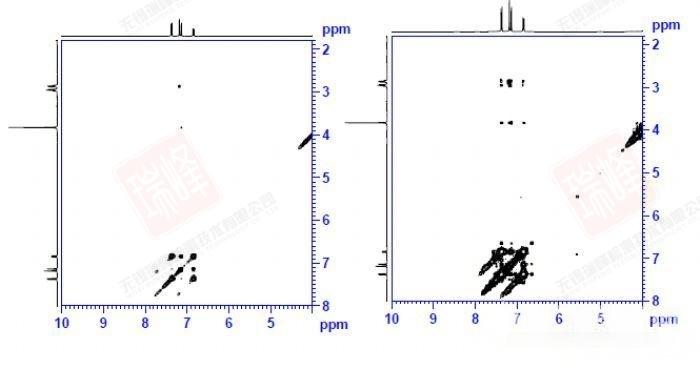
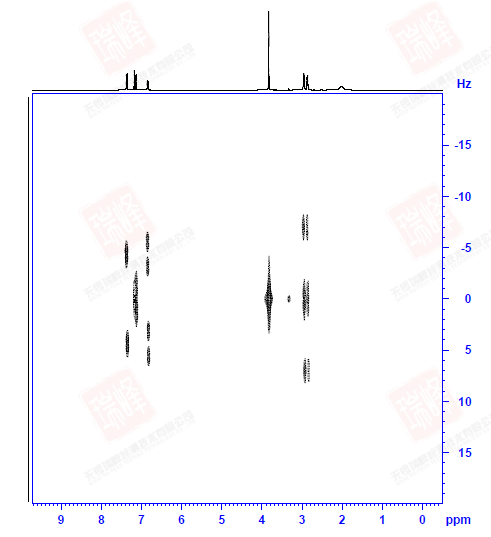
上图是在系统默认0.3秒混合时间以及优化后的1.0秒下所做谱图的对比。在将对角峰调到相近强度时可以看到优化后的谱图(右)交叉峰明显更强。

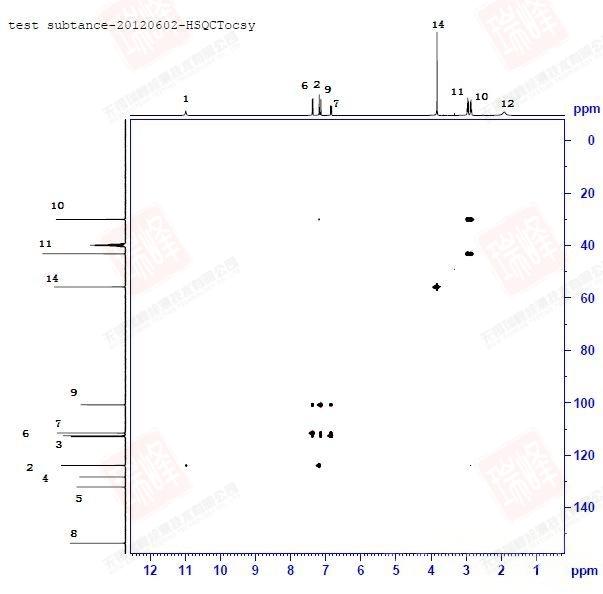
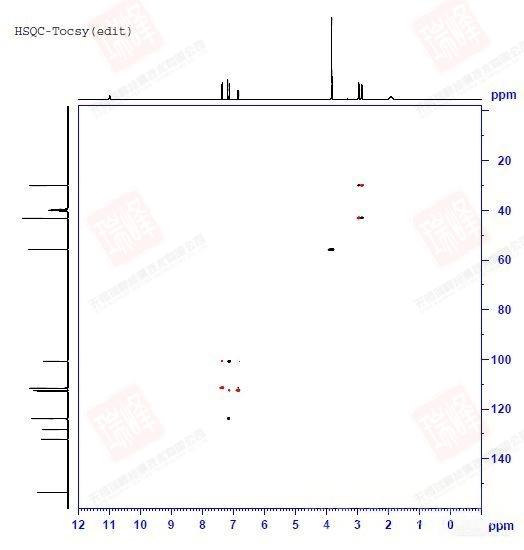
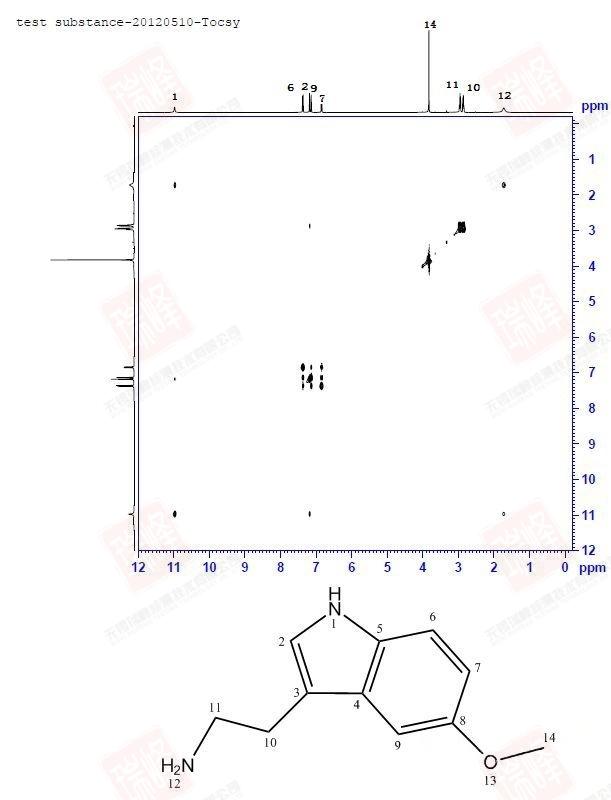
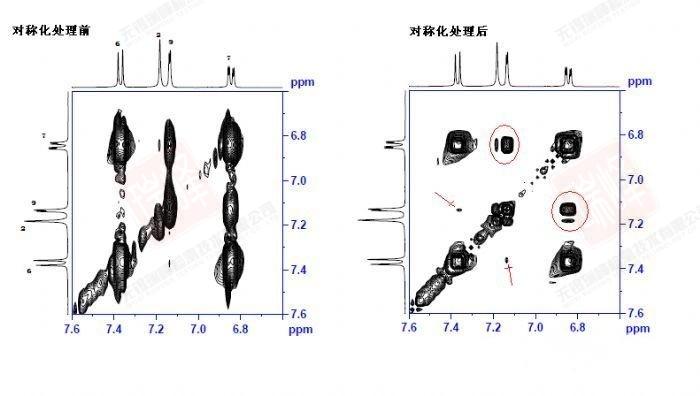
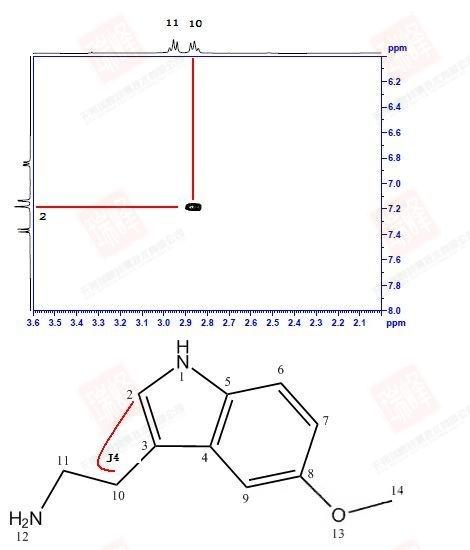
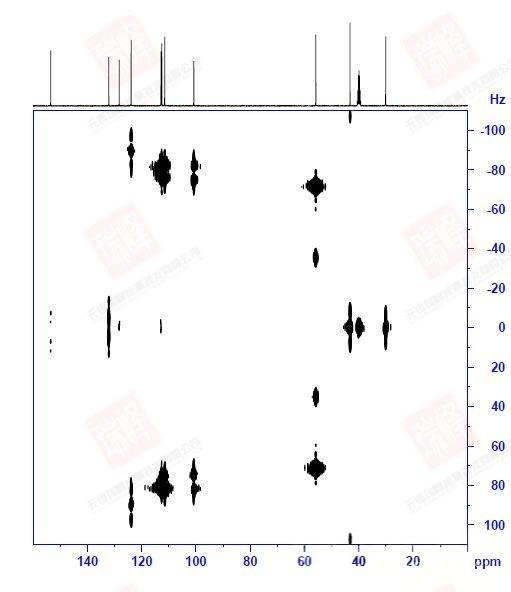
回到一开始给出的NOESY谱图。实际上这一化合物的NOESY并不典型：由于样品浓度很高以及DMSO对于氢键的稳定作用，使得分子内以及分子间围绕着结构中的N和O在氢键作用下形成了各种不同的空间构象。需要强调的是，与依赖键传递的二维谱不同，NOE信号可以在不同分子间传递！因此，当抬高阈值时，我们看到了太多的NOESY信号(下图)

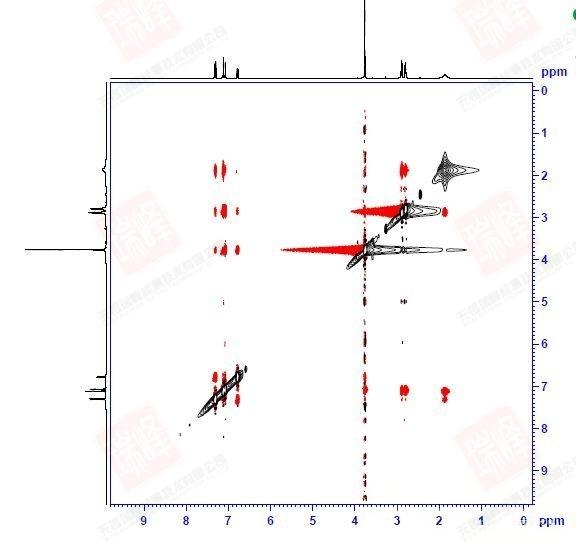
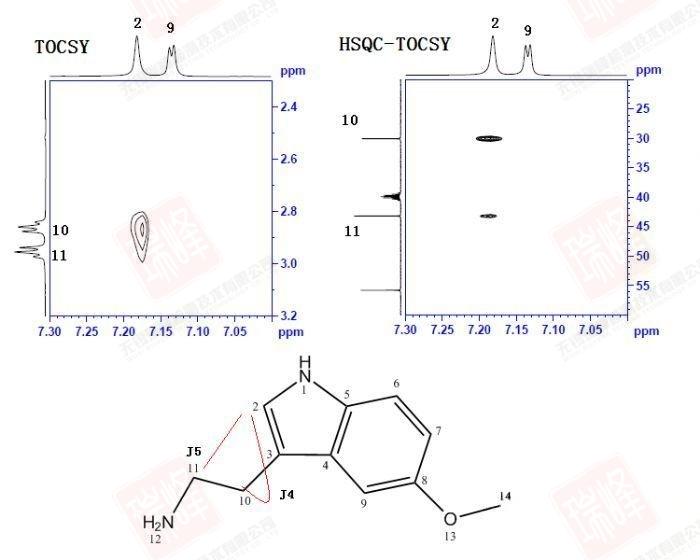
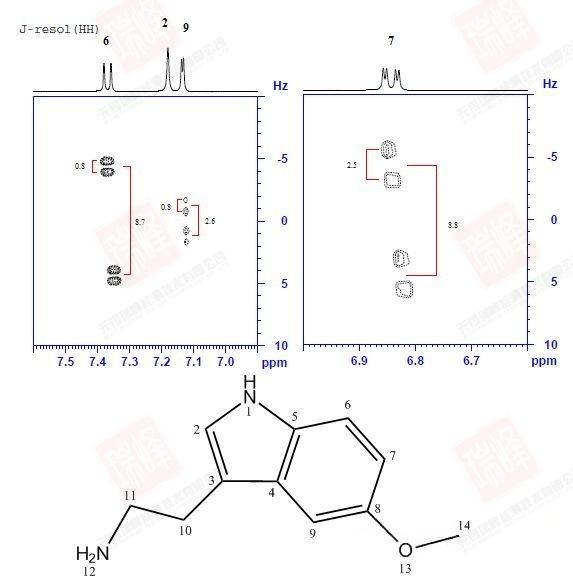
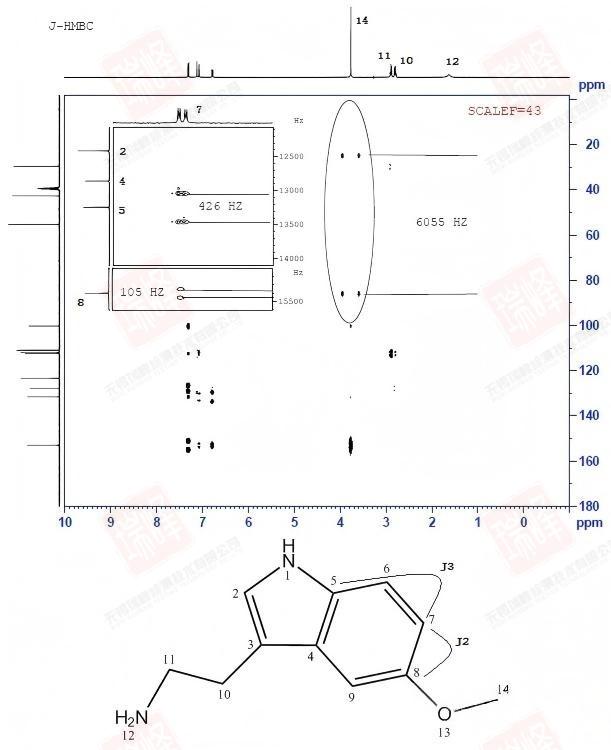
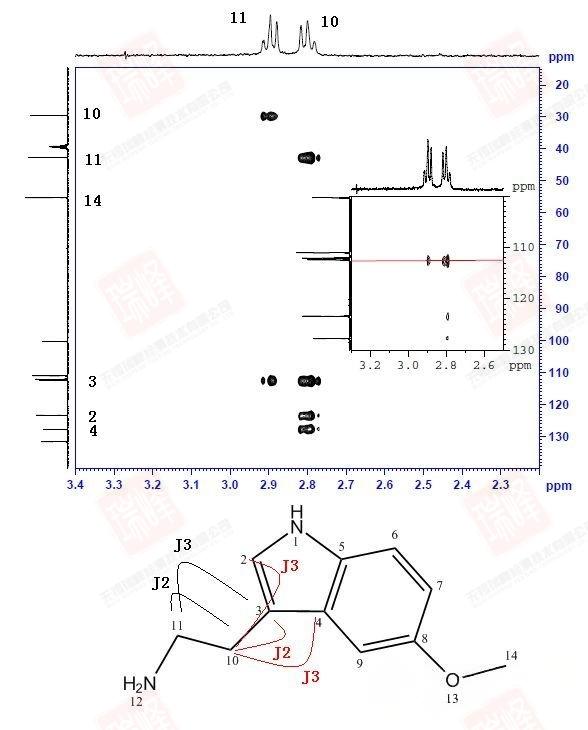
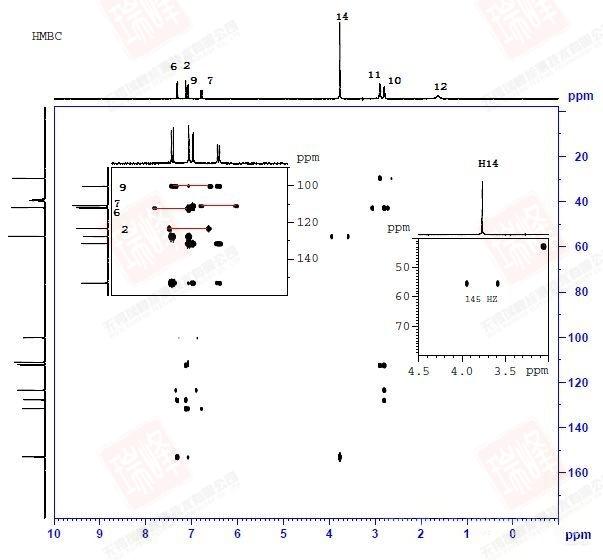
大家可以试着围绕N,O画出两个分子间可能形成的各种氢键连接便能理解这一画面出现的原因了。不过还是可以看到，最强的NOE信号出现在H₆-H₇，H₉-H₁₄以及H₉-H₁₀之间，这暗示着分子内氢键在整个体系中占了最大的比例。

最后要提的一点是，由于脉冲序列相似，NOESY中经常夹杂着COSY信号，这点需要在解谱时予以区分(好在键相近的核空间距离往往接近)。而另外一种用来检测分子内化学交换的谱图(EXSY)和NOESY用的是同一个脉冲序列。

核磁的发展总是迅速得让人惊喜，当我们还在为TOCSY的接力传递赞叹不已时，一种被称为HSQC-TOCSY的二维实验已然将这一系列又推进了一步。与TOCSY相比，HSQC-TOCSY能够在C的维度将原先重叠的信号分开(相较于H,C的谱宽范围很大)，在应对大分子化合物时，这一技术有着相当实用的功效。

如图所示，横向F2维与TOCSY相同，而相关点的纵向F1维是与F2质子处在同一自旋体系中的H直接相连的C的信号。这么说可能有些拗口，结合下面这张图可能更为形象一些。

图中与C直接相连的H经过TOCSY接力传递，将整个自旋体系内的质子与C关联了起来。而这一传递被没有与H相连的C及杂原子(N)所阻断。但这只是理论上的情况，实际操作中我们经常可以看到这一传递会越过这些核传的更远，如本例中的H₆与C₉。

为了便于说明HSQC-TOCSY在重叠峰辨认方面的优势，我将7.0-7.3 ppm处的信号放大如下：

TOCSY中H₂与H₁₀,H₁₁的远程耦合由于后者化学位移的相近而无法区分，但在HSQC-TOCSY中C₁₀与C₁₁在碳谱上完全分开，使得相应的信号不再重叠而变得清晰可辨。在应对复杂结构的化合物时，这一技术会显得更为重要。

需要注意的是，HSQC-TOCSY实验中除了TOCSY信号外，HSQC信号以及少量的HMBC信号会干扰谱图的解析(如图中很强的H₂-C₂信号)。为了排除这部分的干扰，需要结合HSQC实验做出判断。

对于HSQC-TOCSY而言，有一种称为HSQC-TOCSY(edit)的谱图能够将HSQC信号与TOCSY信号分开。

与之前的HSQC-TOCSY谱图相比，”edit”实验将两种信号以相反的相位区分，即使同为HSQC信号，根据C连接H个数的不同，相位也不相同。如图中6-8 ppm处的CH以及甲基的CH₃在图中的HSQC信号以黑色表示，而TOCSY信号为红色；但2-3 ppm中亚甲基的HSQC却是红色，TOCSY则为黑色，HSQC的规律与DEPT135相同。

对于HSQC-TOCSY实验的混合时间对谱图杂峰的影响，我没有比较过，不过至少我觉得有和TOCSY实验相似的效果——混合时间（即自旋锁定时间）越长，信号传得越远但整体信号越弱，具体取值要看实验人员的需要。不过我一般用默认的60ms，下次有机会再做一个系列看下对HSQC-TOCSY的影响。<spin dynamics 2nd>一书中对于混合时间的不同取值对线性4自旋体系在TOCSY中各峰强度的影响有一张不错的比较图，我借过来用一下。其中横坐标是混合时间，纵坐标是各自旋核的信号相对强度。

不过NOESY及HSQC-NOESY 的混合时间取值倒有一个优化的方案，一般与分子的T1时间大致相当。

TOCSY又称全相关谱(Totally Correlation SepctoroscopY)，给出的是某一自旋体系内所有核之间的相关信号。

TOCSY在解谱上与H-H COSY没有任何区别，沿对角峰对称分布着质子之间的相关信号。但不同在于，COSY的相关峰需要质子间有直接的耦合作用，但TOCSY中的相干峰来源于接力相干转移，简而言之在参数设置合适的情况下，TOCSY能比COSY反应相隔更多键的质子之间的关系——前提是这些质子必须在同一自旋体系下。TOCSY的这一奇特性质来源于一种称为“自旋锁定”的脉冲，这一脉冲通过混合期长时间的照射将宏观磁化矢量锁定在y轴从而使得磁化矢量沿着自旋核一个个传递下去：混合期自旋锁定时间越长，相干传递的越远，但弛豫引起的整体信号损失也越大——因此混合时间并不是越长越好。

遗憾的是，这一化合物中TOCSY与COSY相比优势并没有很好地体现出来(之前对称化处理后的COSY过于“霸道”而将TOCSY的信号都出全了，大家有兴趣可以自己做下归属)，为了更好地解释TOCSY与COSY的不同点，请允许我引用<spin dynamics 2nd>一书的两张图做一个简单阐述：

假设有AMX与A’M’X’两个三自旋系统，巧合的是M与M‘的化学位移恰好重叠，由于COSY只能体现A-M,M-X及A’-M’,M’-X’的直接耦合，导致COSY谱无法将这个自旋体系区分开来；但TOCSY的相干传递将A-X及A-X’这块“拼图”补全，从而将两个自旋体系完美地剥离。

最后补充说明的一点是，由于TOCSY与之后要提及的ROESY脉冲序列形式相同(仅自旋锁定时间和锁定脉冲有所区别)，导致在两者之间偶尔夹杂彼此的信号。而ROESY又与EXSY(化学交换谱)相同，因此图中COSY本没有出现的H₁与H₁₂的信号，有可能是NH₂与NH活泼氢相互交换，也可能是两者在空间上相互靠近导致。

与H-H COSY不同，这一实验给出的是C-H直接相关的信息，类似于HSQC或HMQC。但与后者的区别在于，这一实验没有采用反向检测技术，直接采集的是C的信号，因此C维分辨率一般要好于HSQC，但却要付出更多扫描时间的代价。下面给出同一范围内的C-H COSY与HSQC谱图。

很明显可以看到，两种实验在C维和H维分辨率上各有优势，但因为灵敏度的原因，采用反向检测的HSQC在H-C一键关系的指认上用的要广泛的多。

H-H COSY给出的是相邻质子间的耦合关系，是一种非常重要的二维实验。

与之前所介绍的HSQC不同在于，H-H COSY的横向(F2维)和纵向(F1维)表征的都是质子的化学位移，这使得这类谱图呈现与对角线呈对称分布的相关峰(因为耦合作用是相互的，H_a对H_b的耦合等于H_b对H_a)。这一性质在谱图处理中十分有用，后面我会提到经过对称化处理的COSY谱图给出的耦合信息是恐怖的！这类谱图的解谱类似于HSQC，在相关点的横纵两个方向对应的质子存在耦合关系。图中对角线我用红线标示，由于对角峰是同一质子相关，因此并没有任何实际用处，相反由于这部分信号很强常常会严重干扰到化学位移相近的相关峰之间的指认(如图中的6-8 ppm)。早期的相敏COSY实验需要做很好的相位校正来减小对角峰的影响，而DQF-COSY通过过滤掉单自旋的信号使得沿对角峰附近谱图的解释变得更为容易。因此通常而言，如不特殊说明，目前的COSY实验通常为DQF-COSY。

关于二维谱图，我想单独插一句，由于单次采样时间较短以及仪器本身固有的缺陷，COSY等常见的二维谱的信噪比往往比一维要低，虽然可以通过一些软件处理突出我们希望看到的信号，但信号与噪音的区别往往伴随着二维解谱的整个过程。核磁操作人员对于这一点的体会要比解谱人员深刻的多，很多时候谱图一些重要信号的“出”与“不出”只在操作者鼠标滚轮的毫厘之间。我以上图F2维4-10 ppm，F1维2-8 ppm单独放大如下：

在左图的阈值调节下，环上质子之间的耦合关系较为清晰，但其与甲基以及亚甲基之间的相关信息远少于右图相应部分；但右图的阈值调节导致了环上质子相关信号过强而相互干扰，在5-6 ppm之间出现了假信号。由于核磁人员通常为了照顾整张图的信号而必须做出阈值的取舍，因此解谱人员掌握对二维谱图原始数据(topspin的ser文件)的简单处理还是很有必要的。

另一方面，H-H COSY信号的对称性使得对称化处理在谱图的“去伪存真”方面发挥着很重要的作用。以6.6-7.6 ppm的谱图对称化处理前后为例：

从图中可以看到，对称化处理将拥挤的“迷雾”拨开，显露出H₆与H₉之间的J5耦合关系(这与之前J分辨谱的结果一致)，此外，H₂与H₇之间的J6耦合亦得以显现！在大共轭体系下，这类超长距离的耦合关系在COSY中并不罕见。

最后这张图体现了H-H COSY在H归属中的作用：高场氢与H2较强的相关信号暗示了这一氢可能与H₂键隔更短而有较大可能为H₁₀。随后给出的HMBC结果更是增强了这一判断。

异核J分辨谱与同核的解谱方式相同，只不过其F2维是C信号，而F1维给出的是H对C的耦合常数。同样的，为了照顾到所有碳的信号，图中的信号被不合理地放大了，因此显得难以分辨。这里我截取153 ppm处C-8在F1维上的剖面图如下

由于采样时间较短，F1维误差较大，具体值我就不测量了，后面介绍的J-HMBC谱将给出更为精确的C-H耦合常数。不过我们仍然可以从上图初略看到C-8受到H-6，H-9及H-7耦合而呈现的裂分情况。

J-分辨谱在早期曾经是一种非常有用的谱图，它能够很好地区分由于化学位移相近而相互重叠的峰，并将它们的耦合信息在另一个维度加以放大。如上图所示，横向F2维表征了氢谱的出峰位置，而纵向F1维却给出了相应峰在邻核耦合下的裂分情况——很显然，这一裂分比单看氢谱要明显的多，以至于我们可以通过右侧放大的“刻度尺”直接读出相应耦合值。为了便于观察，我将6.6-7.6 ppm的谱图单独放大如下：

从氢谱来看，H-6与H-7 J3耦合,耦合常数8.8 Hz；H-9与H-7的J4耦合，耦合常数2.4 Hz，因此H-6，H-9为d峰，H-7为dd峰。然而通过J-分辨谱，我们观察到了单纯通过氢谱所无法观察到的H-6与H-9 J5耦合的存在，耦合常数0.8 Hz！

不过随着核磁技术的发展，COSY,TOCSY等实验在指认H与H耦合关系中渐渐取代了J分辨谱的地位。如上面提到的H-6和H-9的J5耦合关系，同样可以在之后的TOCSY实验以及对称化处理的COSY谱图中看到。

一种被称为J-HMBC的实验能够给出CH多键耦合常数的信息，这一实验在判定结构(如顺反异构的C-H耦合值差别较大)及优化HMBC参数方面有着重要的作用。

J-HMBC的谱图与HMBC有相似的地方，但不同在于HMBC上的CH相关点沿碳维裂分成了两个，两点间的距离除以放大因子(SCALEF)即为CH远程耦合常数。

以H₇为例，局部图中H₇与C₅的相关点被裂分成了相距426 Hz的两个峰，本实验的SCALEF为43,426/43=9.9 H_Z即为J³_H7C5的值，同样的方法，我们可以算出J²_H7C8约为2.4 Hz，这就很好地解释了在HMBC中H₇与C₅相关点比其与C₆的相关点更强的事实。以此类推，再结合HMBC的CH一键耦合数据，在C13CPD中缺失的CH耦合关系便完美地呈现在了解谱人员的眼前。

需要注意的是，J-HMBC中同样有漏过的CH一键相关信号。图中圆圈标示的6055Hz除以43即为C₁₄与H₁₄的耦合常数141 Hz。这一点在解谱中需要予以区分。

与普通HMBC相比，J-filter后的谱图显得更为清晰(注意，只是J1的相对强度变弱了，有些时候还是能看到部分逃过”筛子”的J1信号，此时要注意区分)。下面我以上图局部为例说明HMBC在结构指认上的作用。

结果如图。可以看到，HMBC使之前较难判断的H₁₀与H₁₁有了新的线索：高场的H由于与C₂与C₄的远程耦合而更接近于H₁₀。之前在H-N HMBC中已经讨论过，HMBC系列对J3经常表现出比J2更大的”偏好“，而J4，J5由于耦合值相似而无法在HMBC上做出明确判断，因此在解HMBC时要较为灵活不能过于教条，要结合多方面的信息做出最为合理的判断。

最后提一点，有一个与需要观察的CH远程耦合值相关的参数对HMBC的实验优化十分重要。比如想要看多键耦合关系，就把这个值调小一点，但这样也将付出整体信号降低的代价。以后有机会我会单独就这个化合物在此参数不同取值下的谱图做一个专帖说明。

H-C HMBC实验给出的是H-C多键耦合的信息。这一谱图的解谱方式与之前介绍的H-N HMBC相似：横向F2维为H，纵向F1维为C，相关点表示F2与F1维的H-C之间J2以上的耦合关系，作为最常见的二维实验之一，H-C HMBC在结构指认上极为重要。

上图为常规HMBC，如果不特殊说明，核磁人员一般给大家的是这种谱图。这种谱图有一个需要注意的地方，由于脉冲中并没有过滤掉CH一键耦合信号，因此在C₁₄所在的F1维化学位移处，沿着H₁₄会对称出现两个小点，两点之间的距离为J1CH的大小(图中145Hz)。这一特征在各氢化学位移离的较远时不会造成太大影响，甚至还能附带给出CH耦合常数，但一旦各H化学位移相近甚至重叠将会对解谱造成一定影响，如图中局部放大的6-8 ppm处，红线连接的即为CH耦合所造成的对称峰，有一些已经与远程耦合的信号叠加在了一起。

因此，我平时更喜欢用一种能去除一键耦合干扰的HMBC实验H-C HMBC(J-filter)。